Chapter 10 Appendix quick pca

10.1 Quck PCA method for snp matrix

See PLoS ONE, 2014, 9:e93766

library(MASS)
N=1000 #sample size
M=2000 #SNP
X=matrix(0, N, M) #SNP matrix

#simulating snp
for(i in 1:M) {
  p1=runif(1, 0.1, 0.9)
  p2=1-p1
  X[1:(N/2),i]=rbinom(N/2, 2, p1)
  X[(N/2+1):N,i]=rbinom(N/2, 2, p2)
}

#conventional PCA
sX=scale(X)
G=sX%*%t(sX)
Geg=eigen(G)
#plot(Geg$vectors[,1], Geg$vectors[,2])


#quick pca
dm=30
sg=matrix(0,dm,dm)
diag(sg)=1
R=mvrnorm(M, rep(0, dm), Sigma=sg)
xt=sX%*%R
ss=apply(xt^2, 2, sum)
Y=matrix(0, nrow(xt), ncol(xt))
for(i in 1:length(ss)) {
  Y[,i]=xt[,i]/ss[i]
}

XtX=sX%*%t(sX)

maxiter=10
for(it in 1:maxiter) {
  xxt=XtX%*%Y
  ss1=apply(xxt^2, 2, sum)
  
  for(i in 1:length(ss1)) {
    Y[,i]=xxt[,i]/ss1[i]
  }
}

QR=qr.default(Y)
B=t(QR$qr)%*%sX
S=B%*%t(B)

eg=eigen(S)

U=QR$qr %*% eg$vectors
D=sqrt(eg$values/(N-1))  
P=U*D

par(mfrow = c(1,2))
plot(main="PCA", xlab="eVec 1", ylab="eVec 2", Geg$vectors[,1], Geg$vectors[,2])
plot(main="Quick PCA", xlab="eVec 1", ylab="eVec 2", U[,1], U[,2])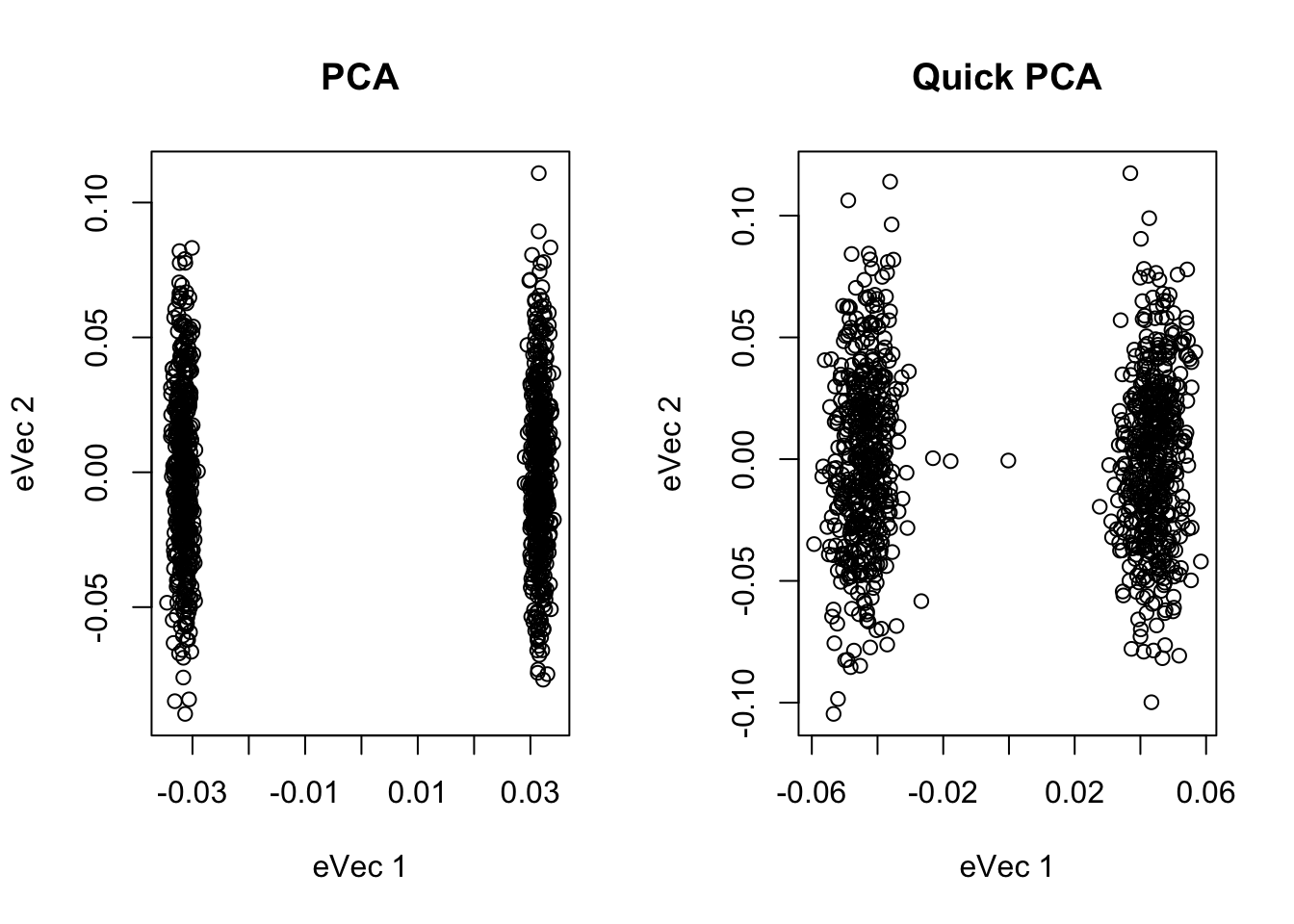

cor(Geg$vectors[,1], U[,1])

## [1] 0.9929008

The procedure in Galinsky (AJHG)

library(Rcpp)
sourceCpp("~/git/Notes/R/RLib/Shotgun.cpp")
M=10000
N=500
L=20
I=5

frq=runif(M, 0.1, 0.3)
Dp=sample(c(runif(M/2, 0, 0), runif(M/2, 0, 0)), M)
Dp=Dp[-1]

fst=0.02
frq1=rbeta(M, frq*(1-fst)/fst, (1-frq)*(1-fst)/fst)
frq2=rbeta(M, frq*(1-fst)/fst, (1-frq)*(1-fst)/fst)

G1=GenerateGenoDprimeRcpp(frq1, Dp, N)
G2=GenerateGenoDprimeRcpp(frq2, Dp, N)

G=rbind(G1, G2)

s=apply(G, 2, scale)
ss=s%*%t(s)/M
sE=eigen(ss)

G0=matrix(rnorm(nrow(s)*L), nrow(s), L)
HH=matrix(0, M, (I+1)*L)
for(i in 0:(I-1)) {
  H=t(s) %*% G0
  G0=s%*%H/M
  HH[,(i*L+1):((i+1)*L)]=H
}

svd_h=svd(HH)
Ty=t(svd_h$u)%*%t(s)
svd_t=svd(Ty)

layout(matrix(1:2, 1, 2))
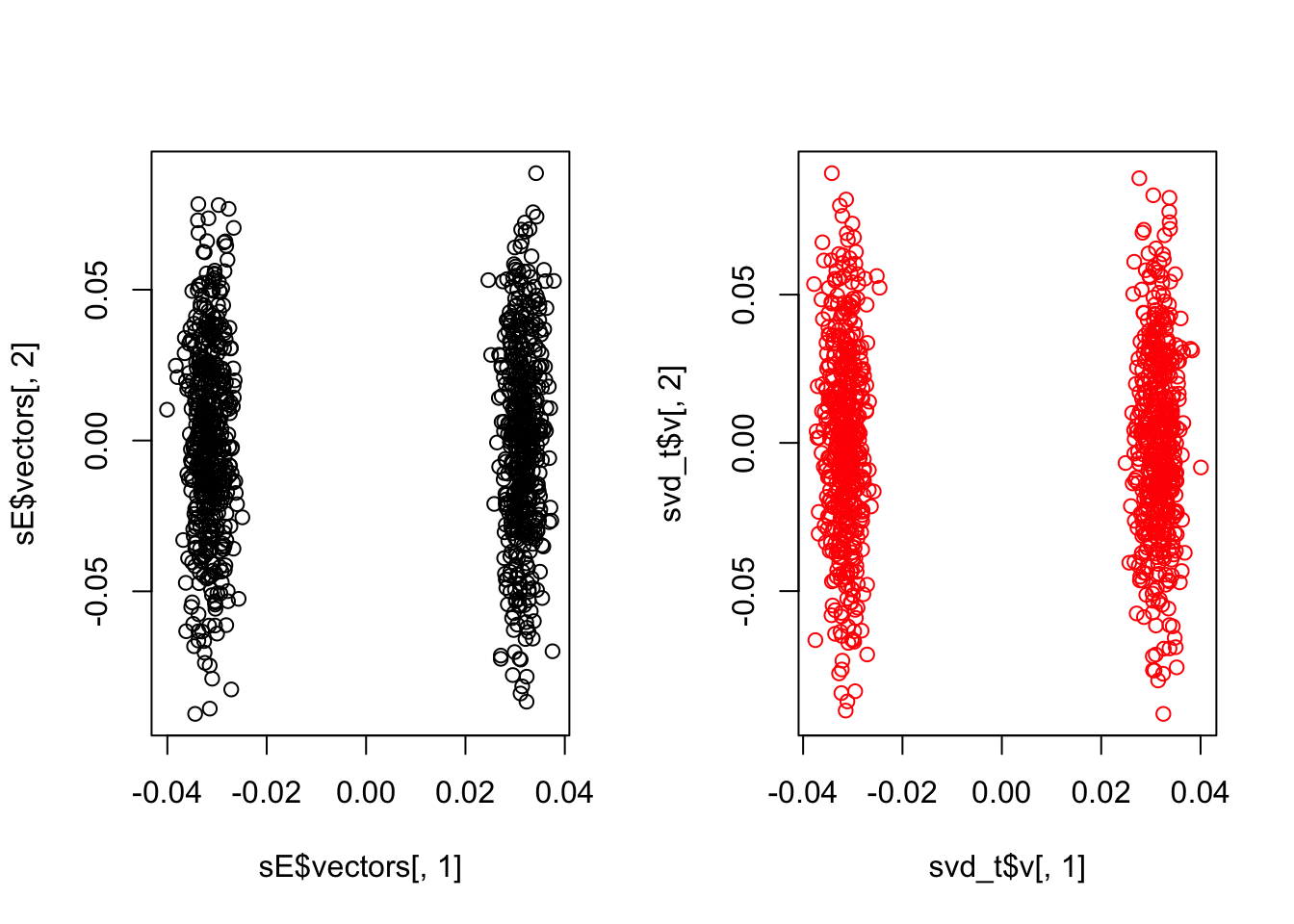
plot(sE$vectors[,1], sE$vectors[,2])

plot(svd_t$v[,1], svd_t$v[,2], col="red")